Задание 6.53 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 107

МNKS - четырехугольник с вершинами

М(-9, -3), N(-3; -3;), K(-3; -7), S(-9; -7).

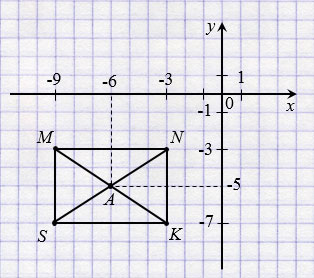
а) Четырехугольник МNKS - прямоугольник.

б) Единичный отрезок - 1 дм.

Периметр МNKS - ?

Площадь МNKS - ?

Р = 2 • (МN + NK) = 2 • (6 + 4) =

= 2 • 10 = 20 (дм).

S = МN • NK = 6 • 4 = 24 (дм²).

Ответ: периметр прямоугольника МNKS равен 14 дм, площадь - 12 дм².

в) Точка пересечения отрезков МK и NS:

А(-6; -5).

Пояснения:

Чертим прямоугольную систему координат с единичным отрезком 1 клетка. Отмечаем в этой системе координат точки М(-9, -3), N(-3; -3;), K(-3; -7), S(-9; -7).

Чтобы попасть в точку М с координатами (-9; -3), нужно сначала пройти по оси 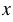от начала отсчета влево на 9 единиц, а потом - на 3 единицы вниз.

Чтобы попасть в точку N с координатами (-3; -3), нужно сначала пройти по оси 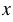от начала отсчета влево на 3 единицы, а потом - на 3 единицы вниз.

Чтобы попасть в точку K с координатами (-3; -7), нужно сначала пройти по оси 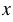от начала отсчета влево на 3 единицы, а потом - на 7 единицы вниз.

Чтобы попасть в точку S с координатами (-9; -7), нужно сначала пройти по оси 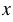от начала отсчета влево на 9 единиц, а потом - на 7 единиц вниз.

Соединив точки М, N, K и S получаем четырехугольник МNKS.

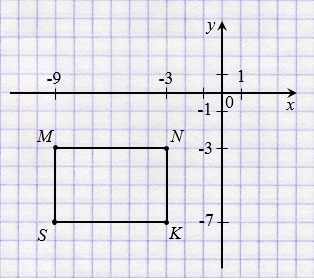
а) Четырехугольник МNKS является прямоугольником, так как все его углы прямые.

б) По условию длина единичного отрезка равна 1 дм (в нашем случае единичные отрезок - это длина одной клетки), значит, длина полученного четырехугольника      МN = 6 дм, а ширина NK = 4 дм.

Периметр прямоугольника равен удвоенной сумме его соседних сторон (длины и ширины), значит, периметр прямоугольника МNKS:

Р = 2 • (МN + NK) = 2 • (6 + 4) =

= 2 • 10 = 20 (дм).

Площадь прямоугольника равна произведению его соседних сторон (длины и ширины, значит, площадь прямоугольника МNKS:

S = МN • NK = 6 • 4 = 24 (дм²).

Далее с помощью линейки проводим отрезки МK и NS, которые пересекаются в точке А. Чтобы определить координаты точки, нужно опустить из этой точки перпендикуляры на ос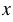и и 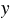, которые и укажут координаты данной точки. Значит, точка А имеет координаты (-6; -5), т.е. А(-6; -5).