Задание П.52. Вопросы и задачи на повторение. Задачи - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2. Страница 165
Старая и новая редакции
Вернуться к содержанию учебника
Вопросы и задачи на повторение. Задачи. Страница 165
Вопрос
№П.52 учебника 2023-2024 (стр. 165):
От двух станций, расстояние между которыми 312,5 км, одновременно навстречу друг другу вышли товарный и пассажирский поезда и встретились через 2,5 ч. С какой скоростью двигались поезда, если скорость пассажирского поезда была в 1,5 раза больше скорости товарного поезда
Подсказка
№П.52 учебника 2023-2024 (стр. 165):
Вспомните:
- Задачи на движение.
- Что называют уравнением, его корни.
- Сложение десятичных дробей.
- Умножение десятичных дробей (распределительное свойство).
- Деление десятичных дробей.
Ответ
№П.52 учебника 2023-2024 (стр. 165):
1)  + 1,5
+ 1,5 = (1 + 1,5)
= (1 + 1,5) = 2,5
= 2,5 (км/ч) - скорость сближения поездов.
(км/ч) - скорость сближения поездов.
2) 2,5 • 2,5 = 312,5
= 312,5
6,25 = 312,5
= 312,5
 = 312,5 : 6,25
= 312,5 : 6,25
 = 31 250 : 625
= 31 250 : 625
 = 50
= 50
|
|
50 км/ч - скорость товарного поезда.
50 • 1,5 = 75 (км/ч) - скорость пассажирского поезда.
| × | 1 | 5 | |
| 5 | 0 | ||
| 7 | 5 | 0 |
Ответ: 50 км/ч и 75 км/ч.
Пояснения:
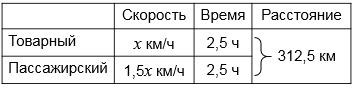
По условию задачи составляем краткую запись в виде таблицы (смотри выше).
Пусть скорость товарного поезда равна  км/ч. Скорость пассажирского поезда была в 1,5 раза больше скорости товарного поезда, значит, скорость пассажирского поезда равна 1,5
км/ч. Скорость пассажирского поезда была в 1,5 раза больше скорости товарного поезда, значит, скорость пассажирского поезда равна 1,5 км/ч.
км/ч.
Поезда движутся навстречу друг другу, поэтому можно найти скорость их сближения, сложив их скорости, получим:
 + 1,5
+ 1,5 = (1 + 1,5)
= (1 + 1,5) = 2,5
= 2,5 (км/ч).
(км/ч).
При выполнении преобразований использовали распределительное свойство умножения (переменную  вынесли за скобки).
вынесли за скобки).
Поезда двигались навстречу друг другу со скоростью сближения 2,5 км/ч и встретились через 2,5 ч. При этом изначально между поездами было 312,5 км. Чтобы найти расстояние, нужно скорость умножить на время. Получается, можем составить следующее уравнение:
км/ч и встретились через 2,5 ч. При этом изначально между поездами было 312,5 км. Чтобы найти расстояние, нужно скорость умножить на время. Получается, можем составить следующее уравнение:
2,5 • 2,5 = 312,5 или, выполнив умножение в левой части уравнения,
= 312,5 или, выполнив умножение в левой части уравнения,
6,25 = 312,5.
= 312,5.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда:
 = 312,5 : 6,25,
= 312,5 : 6,25,
 = 31 250 : 625,
= 31 250 : 625,
 = 50.
= 50.
Учитывая обозначения, введенные выше, скорость товарного поезда равна 50 км/ч.
Скорость пассажирского поезда в 1,5 раза больше скорости товарного поезда, значит, скорость пассажирского поезда равна:
50 • 1,5 = 75 (км/ч).
Правила, по которым выполнены вычисления, смотрите в подсказке.
Вернуться к содержанию учебника