Задание 1.63 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 1. Страница 19
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№1.63 учебника 2023-2024 (стр. 19):
№1.63 учебника 2021-2022 (стр. 19):
Ширина прямоугольника в 4 раза меньше его длины. Найдите периметр прямоугольника, если ширина равна 28 см.
Подсказка
№1.63 учебника 2023-2024 (стр. 19):
№1.63 учебника 2021-2022 (стр. 19):
Вспомните:
- Оформление задач.
- Что называют прямоугольником, как найти его периметр.
Ответ
№1.63 учебника 2023-2024 (стр. 19):
№1.63 учебника 2021-2022 (стр. 19):
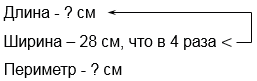
1) 28 • 4 = 112 (см) - длина прямоугольника.
| × | 2 | 8 |
| 4 | ||
| 1 | 1 | 2 |
2) 2 • (112 + 28) = 2 • 140 = 280 (см).
Ответ: периметр прямоугольника равен 280 см.
Пояснения:
По условию ширина прямоугольника равна 28 см и также ширина в 4 раза меньше, чем длина прямоугольника, значит, длина прямоугольника в 4 раза больше, чем ширина. Тогда, чтобы найти длину, необходимо ширину умножить на 4, значит, длина прямоугольника:
28 • 4 = 112 (см).
Участок имеет форму прямоугольника, значит, длина забора, которым нужно огородить этот участок, равна периметру этого прямоугольника.
Периметр прямоугольника равен сумме длин четырех его сторон или, учитывая то, что в прямоугольнике противолежащие стороны равны, удвоенной сумме двух его измерений (длины и ширины). Получается, если 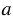 и
и 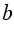 соответственно длина и ширина прямоугольника, то его периметр:
соответственно длина и ширина прямоугольника, то его периметр:
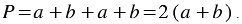
Итак, длина прямоугольника - 112 см, ширина - 28 см, значит, периметр прямоугольника:
2 • (112 + 28) = 2 • 140 = 280 (см).
Вернуться к содержанию учебника