Задание 18. Вопросы для повторения к главе II - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопросы для повторения к главе II. Страница 49, 50
Вопрос
№18 учебника 2013-2022 (стр. 49):
№18 учебника 2023-2024 (стр. 50):
Объясните, как отложить от данного луча угол, равный данному.
Подсказка
№18 учебника 2013-2022 (стр. 49):
№18 учебника 2023-2024 (стр. 50):
Вспомните:
- Что такое луч.
- Что называется углом.
- Что такое окружность.
- Как построить угол, равный данному.
Ответ
№18 учебника 2013-2022 (стр. 49):
№18 учебника 2023-2024 (стр. 50):
Дано: луч ОМ, 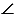 А.
А.
Отложить: от луча ОМ угол, равный 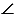 А.
А.
Решение:
Произвольно строим с помощью линейки 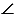 А и луч ОА.
А и луч ОА.
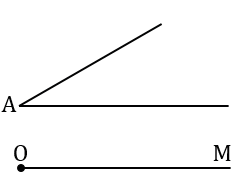
Строим с помощью циркуля окружность произвольного радиуса с центром в вершине 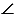 А.
А.
Точки пересечения окружности со сторонами  А обозначаем В и С, соединяем их с помощью линейки.
А обозначаем В и С, соединяем их с помощью линейки.
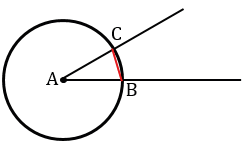
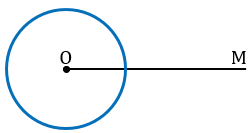
Построим с помощью циркуля окружность того же радиуса, как и окружность с центром в вершине 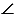 А, от начала луча ОМ точке О.
А, от начала луча ОМ точке О.
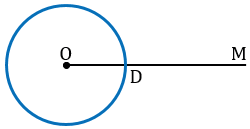
Точку пересечения данной окружности с лучом ОМ обозначим D.
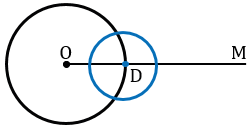
Теперь строим с помощью циркуля окружность радиуса ВС с центром в точке D.
Получаем окружности с центрами в точках О и D пересекаются в двух точках, обозначим одну из этих точек Е.
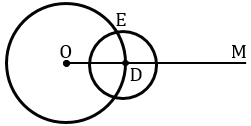
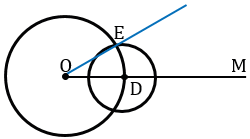
С помощью линейки проведем луч ОЕ. И получаем 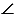 МОЕ =
МОЕ =  А, что и нужно было построить.
А, что и нужно было построить.
Вернуться к содержанию учебника