Задание 92 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник. Страница 31
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№92 учебника 2013-2022 (стр. 31):
Периметр одного треугольника больше периметра другого. Могут ли быть равными эти треугольники?
№92 учебника 2023-2024 (стр. 31):
Начертите треугольник и обозначьте его вершины буквами M, N и P. а) Назовите все углы и стороны треугольника; б) с помощью масштабной линейки измерьте стороны и найдите периметр треугольника.
Подсказка
№92 учебника 2013-2022 (стр. 31):
Вспомните:
- Что такое треугольник и как найти его периметр.
- Какие треугольники называются равными.
№92 учебника 2023-2024 (стр. 31):
Вспомните:
- Что такое треугольник.
- Элементы треугольника.
- Как найти периметр треугольника.
Ответ
№92 учебника 2013-2022 (стр. 31):
Ответ: Если периметр одного треугольника больше периметра другого, равными эти треугольники быть не могут.
Пояснения:
Предположим, что треугольники равны. Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Периметр треугольника - это сумма длин трех его сторон. Так как стороны у равных треугольников соответственно равны, то сумма их длин будет одинакова для обоих треугольников, т.е. будут равны их периметры, а это противоречит условию, а, значит, наше предположение неверно и данные треугольники не могут быть равными.
№92 учебника 2023-2024 (стр. 31):
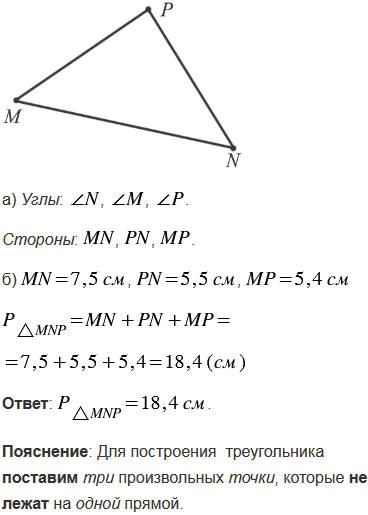

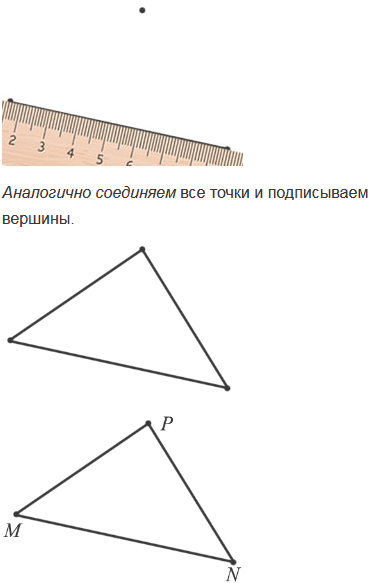
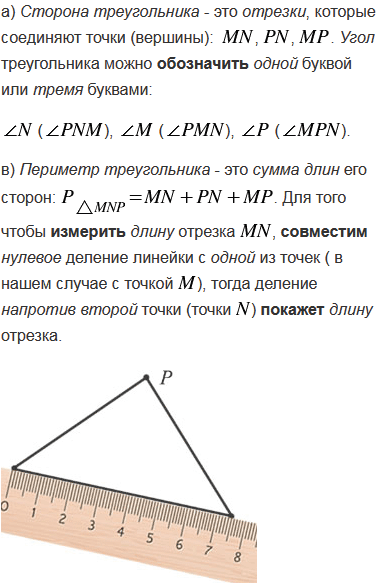
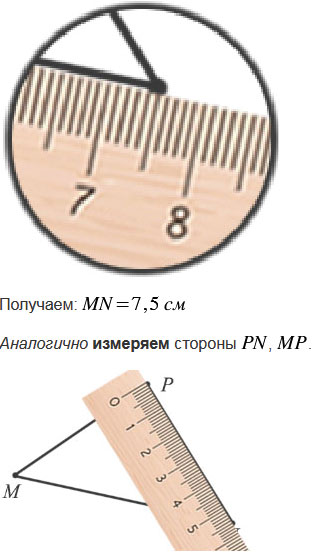
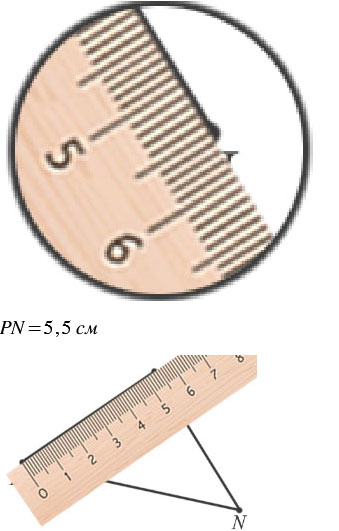

Вернуться к содержанию учебника