Номер 482 - ГДЗ Алгебра 8 класс. Мерзляк, Полонский. Учебник. Страница 122

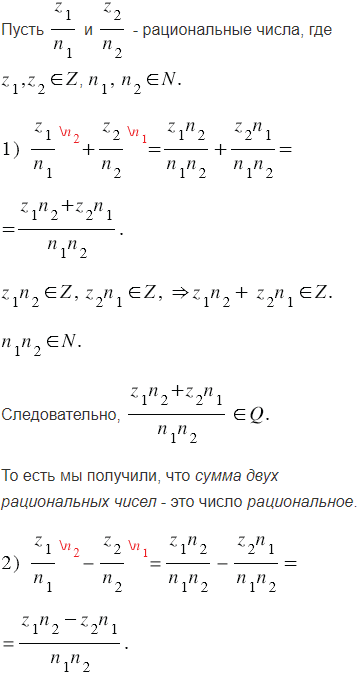
Пояснения:

Каждое рациональное число можно представить в виде отношения 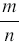, где 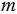- целое число, а 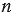- натуральное. Тогда используя правила сложения, вычитания, умножения и деления обыкновенных дробей, мы должны получить дробь такого же вида.

Чтобы сложить (вычесть) две дроби с разными знаменателями, надо:

1) привести данные дроби к общему знаменателю;

2) применить правило сложения (вычитания) дробей с одинаковыми знаменателями.

Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.

Чтобы найти разность двух дробей с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.

Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей.

Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное делителю.

При этом помним, что натуральные числа еще называют положительными целыми числами, а противоположные числа - это два числа, которые отличаются друг от друга только знаками.

Все натуральные числа образуют множество натуральных чисел. Данное множество обозначается буквой N.

Все натуральные числа, противоположные им числа и число нуль образуют множество целых чисел. Данное множество обозначают буквой Z.

Целые и дробные (как положительные, так и отрицательные) числа образуют множество рациональных чисел. Данное множество обозначают буквой Q.