1. Главная
  2. ГДЗ
  3. 4 класс
  4. Математика
  5. Волкова, Моро рабочая тетрадь
  6. 26. Часть 1

Страница 26 - ГДЗ Математика 4 класс. Волкова, Моро. Рабочая тетрадь часть 1

Старая и новая редакции

Вернуться к содержанию рабочей тетради

23 24 25 26 27 28 29

Вопрос

35.

Ответ

Пояснения:

Повтори состав многозначного числа.

Каждое следующее число образуется путём прибавления единицы к предыдущему числу, а каждое предыдущее число получается путем вычитания единицы из последующего числа.

23 24 25 26 27 28 29

Вопрос

36.

c 540 1200 480   280
k 60 100   5 7
c : k     6 100  

Подсказка

Повтори, как называются числа при делении, как умножать и делить круглые числа.

Ответ

Решение

c 540 1200 480 500 280
k 60 100 80 5 7
c : k 9 12 6 100 40

Пояснение

540 : 60 = 9

1200 : 100 = 12

480 : 6 = 80

100 • 5 = 500

280 : 7 = 40

23 24 25 26 27 28 29

Вопрос

37. Вычисли значение первого выражения. В остальных расставь скобки так, чтобы в каждом следующем выражении получалось другое значение.

Подсказка

Повтори материал о порядке действий и действиях со скобками.

Ответ

Решение

Пояснение

56 - 6 : 2 • 5 = 41

1) 6 : 2 = 3

2) 3 • 5 = 15

3) 56 - 15 = 41

(56 - 6) : 2 • 5 = 125

1) 56 - 6 = 50

2) 50 : 2 = 25

3) 25 • 5 = 20 • 5 + 5 • 5 = 125

(56 - 6) : (2 • 5) = 5

1) 56 - 6 = 50

2) 2 • 5 = 10

3) 50 : 10 = 5

(56 - 6 : 2) • 5 = 260

1) 6 : 2 = 3

2) 56 - 3 = 53

3) 53 • 5 = 50 • 5 + 3 • 5 = 265

23 24 25 26 27 28 29

Вопрос

38. 1) Запиши в таблице, какими могут быть длины двух разных сторон прямоугольника, если его периметр равен 20 см.

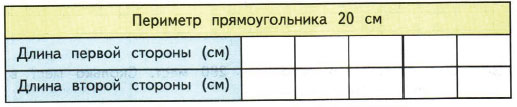
2) Какой из этих прямоугольников имеет наибольшую площадь? Закрась нужный столбик.

Подсказка

Повтори, как найти периметр и площадь прямоугольника.

Ответ

Решение

Пояснение

1) Периметр прямоугольника - это сумма длин всех его сторон. Мы знаем, что противоположные стороны прямоугольника равны. Поэтому, вычисляя периметр, можно сумму длины и ширины умножать на 2. Значит, чтобы найти сумму длины и ширины, нужно периметр разделить на 2:

20 : 2 = 10 (см)

Нужно подобрать такие длины первой и второй стороны, чтобы их сумма равнялась 10:

9 + 1 = 10 (см)

8 + 2 = 10 (см)

7 + 3 = 10 (см)

6 + 4 = 10 (см)

5 + 5 = 10 (см)

2) Чтобы найти площадь прямоугольника, нужно его длину умножить на ширину:

9 • 1 = 9 (см2)

8 • 2 = 16 (см2)

7 • 3 = 21 (см2)

6 • 4 = 24 (см2)

5 • 5 = 25 (см2)

Наибольшая площадь у прямоугольника со сторонами 5 см. Этот прямоугольник - квадрат.

23 24 25 26 27 28 29

Вернуться к содержанию рабочей тетради