Задание 4.192 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 40
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№4.192 учебника 2021-2022 (стр. 40):
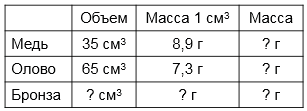
Для получения серой бронзы сплавили кусок меди объемом 35 см3 и кусок олова объемом 65 см3. Чему равна масса 1 см3 бронзы, если масса 1 см3 меди 8,9 г, а масса 1 см3 олова 7,3 г? Результат округлите до десятых долей грамма. (Бронза - один из первых освоенных человеком сплавов металлов.)
Подсказка
№4.192 учебника 2021-2022 (стр. 40):
Вспомните:
- Умножение десятичных дробей.
- Сложение десятичных дробей.
- Округление десятичных дробей.
Ответ
№4.192 учебника 2021-2022 (стр. 40):
1) 8,9 • 35 = 311,5 (г) - масса меди в сплаве.
| × | 8 | 9 | ||
| 3 | 5 | |||
| + | 4 | 4 | 5 | |
| 2 | 6 | 7 | ||
| 3 | 1 | 1 | 5 |
2) 7,3 • 65 = 474,5 (г) - масса олова в сплаве.
| × | 7 | 3 | ||
| 6 | 5 | |||
| + | 3 | 6 | 5 | |
| 4 | 3 | 8 | ||
| 4 | 7 | 4 | 5 |
3) 311,5 + 474,5 = 786 (г) - масса бронзы.
| + | 3 | 1 | 1 | , | 5 |
| 4 | 7 | 4 | , | 5 | |
| 7 | 8 | 6 | , | 0 |
4) 35 + 65 = 100 (см3) - объем бронзы.
5) 786 : 100 = 7,86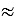 
7,9 (г)
Ответ: масса 1 см3 бронзы 7,9 г.
Пояснения:
Чтобы найти массу каждого металла в сплаве, надо умножить объём данного металла на массу 1 см3, получим, что в сплаве 8,9 • 35 = 311,5 (г) меди и
7,3 • 65 = 474,5 (г) олова.
Чтобы найти массу сплава, надо сложить массу меди и олова, которые использовали для сплава, то есть масса сплава (бронзы):
311,5 + 474,5 = 786 (г).
Чтобы найти общий объём сплава (бронзы), надо сложить объём меди и объём олова, используемые для сплава, то есть объём сплава (бронзы):
35 + 65 = 100 (см3).
Чтобы найти массу 1 см3 сплава (бронзы), надо массу сплава разделить на его объём, получаем, что масса 1см3 сплава (бронзы) равна:
786 : 100 = 7,86 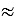7,9 (г).
Правила, по которым выполнены вычисления и округление, смотрите в подсказке.
Вернуться к содержанию учебника