Задание 6.69 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 108

а) МNP - прямоугольный треугольник с прямым углом N.

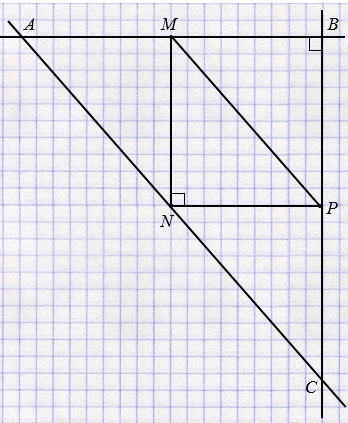
АВ || NP, BC || NM, AC || MP.

АВС - прямоугольный треугольник с прямым углом В.

б) DF АС, KТ АС.

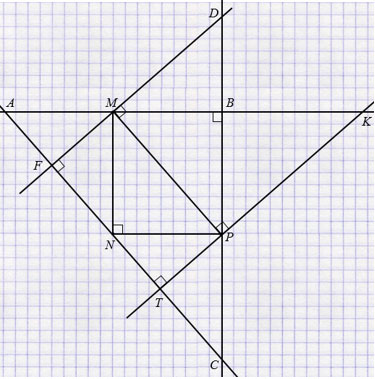
Получилось 13 прямоугольных треугольников:

АМF, АВС, АKТ, АМN, FMN, FDС, МВD, МВР, МNP, МKP, ВKP, РТС, NPТ.

Пояснения:

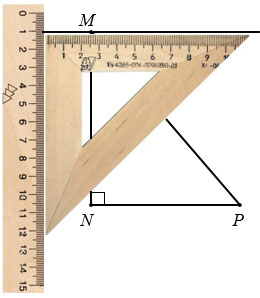
а) С помощью чертежного треугольника чертим прямоугольный треугольник МNP с прямым углом N. Сначала чертим отрезок NP, к этому отрезку прикладываем чертежный треугольник так, чтобы одна его сторон, образующих прямой угол лежала вдоль отрезка NP, при этом вершина прямого угла чертежного треугольника должна совпадать с точкой N. Вдоль другой стороны чертежного треугольника чертим отрезок NM.

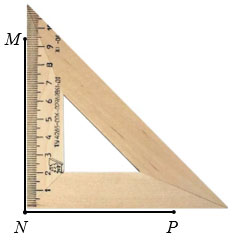
Далее соединяем точки М и Р, получаем прямоугольный треугольник МNP с прямым углом N.

С помощью чертежного треугольника и линейки построим прямую параллельную стороне NP, проходящую через точку М. Для этого прикладываем чертежный треугольник одной из его сторон, образующих прямой угол, к стороне NP, вдоль другой стороны треугольника, образующей прямой угол, прикладываем линейку.

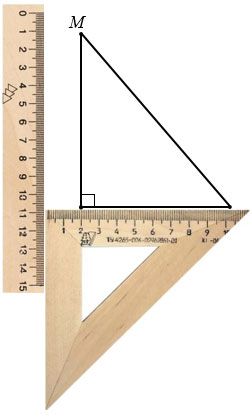
Далее вдоль линейки, не меняя ее положения, смещаем чертежный треугольник до точки М и через точку М вдоль стороны чертежного треугольника чертим прямую.

Аналогично через вершины N и Р чертим прямые параллельные сторонам МР и NM соответственно. Точки пересечения построенных прямых обозначаем буквами А, В и С.

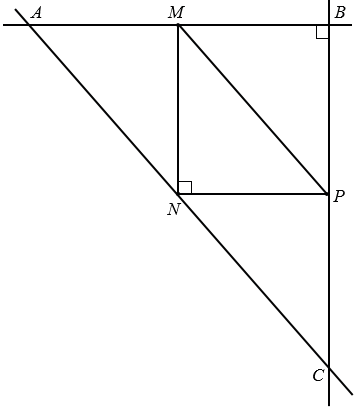
Мы получили прямоугольный треугольник АВС с прямым углом В.

б) С помощью чертежного угольника строим прямую, проходящую через вершину М, перпендикулярную стороне АС треугольника АВС. Для этого прикладываем чертежный треугольник так, чтобы одна его сторон, образующих прямой угол лежала вдоль стороны АС, при этом точка М лежала вдоль другой стороны чертежного треугольника, образующей прямой угол. Через точку М вдоль стороны треугольника чертим прямую, которая и будет перпендикулярна стороне АС.

Аналогично, через вершину Р строим прямую, проходящую через вершину Р, перпендикулярную стороне АС треугольника АВС.

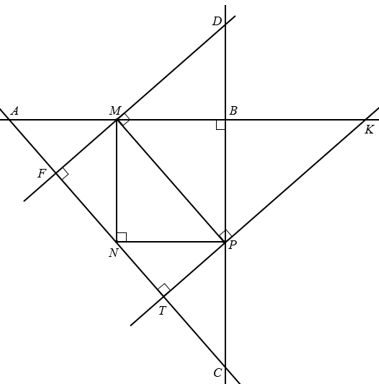
Точки пересечения прямых обозначили буквами Т, Е, F и D. Обратите внимание, углы DMP и МРK прямые, так по построению в пункте а) прямые АС и МР параллельны, а прямая перпендикулярная к одной из параллельных прямых перпендикулярна и к другой параллельной прямой.

По рисунку видим, что получилось 13 прямоугольных треугольников:

АМF, АВС, АKТ, АМN, FMN, FDС, МВD, МВР, МNP, МKP, ВKP, РТС, NPТ.