стр. 104. Проверьте себя - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Проверьте себя
Вопрос
Проверочная работа
1. На рисунке 6.18 изображены прямые 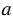 ,
, 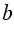 ,
,  ,
, 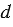 и
и 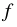 .
.
а) Какие прямые параллельны?
б) Какие прямые пересекаются?
в) Есть ли на рисунке перпендикулярные прямые?
Если да, запишите все пары перпендикулярных прямых.
2. Начертите прямоугольный треугольник АВС с прямым углом В. Какие из утверждений верны?
а) Прямые АВ и ВС пересекаются.
б) Прямые АВ и ВС перпендикулярны.
в) Прямые АВ и ВС параллельны.
г) Прямые АС и ВА перпендикулярны.
д) Прямые АС и ВА пересекаются.
е) Прямые ВС и АС пересекаются.
ж) Прямые ВС и АС не перпендикулярны.
3. Начертите четырехугольник РQRT, у которого:
а) РQ || RT;
б) РQ || RT, PT || RQ и PT 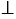 RT.
RT.
Подсказка
Вспомните:
Ответ
Проверочная работа
1. а) Параллельны прямые:

б) Пересекаются прямые:
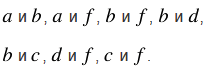
в) Перпендикулярные прямые:
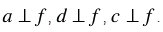
2. Треугольник АВС - прямоугольный,
 В - прямой.
В - прямой.
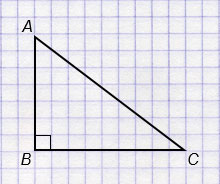
а) Прямые АВ и ВС пересекаются - верно.
б) Прямые АВ и ВС перпендикулярны - верно.
в) Прямые АВ и ВС параллельны - неверно.
г) Прямые АС и ВА перпендикулярны - неверно.
д) Прямые АС и ВА пересекаются - верно.
е) Прямые ВС и АС пересекаются - верно.
ж) Прямые ВС и АС не перпендикулярны - верно.
3. а) РQRT - четырехугольник.
РQ || RT
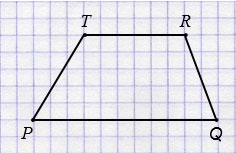
б) РQRT - четырехугольник.
РQ || RT, PT || RQ и PT 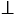 RT.
RT.
Пояснения:
Две непересекающиеся прямые на плоскости называют параллельными.
Перпендикулярные прямые - это прямые, которые при пересечении образуют четыре прямых угла.
Прямые пересекаются, если у них есть общая точка (при этом помним то, что прямые всегда можно продолжить).
3. а) Начертим четырехугольник РQRT, у которого РQ || RT.
Начертим произвольный отрезок РQ.
Далее построим прямую параллельную PQ. Чтобы провести прямую параллельную отрезку РQ, прикладываем чертежный треугольник к отрезку PQ одной из его сторон образующих прямой угол, а вдоль другой стороны чертежного треугольника, образующей прямой угол, прикладываем линейку.

Не меняя положения линейки, двигаем вдоль нее чертежный треугольник на произвольное расстояние и проводим прямую вдоль стороны чертежного треугольника, которая и будет параллельна РQ.
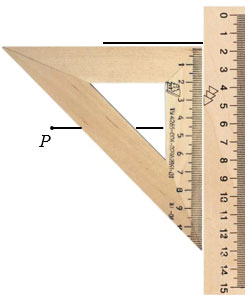
На построенной прямой отмечаем точки Т и R и соединяем точки Р и Т, Q и R.
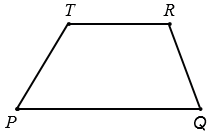
Мы получили четырехугольник РQRT, у которого РQ || RT.
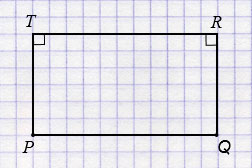
б) Начертим четырехугольник РQRT, у которого РQ || RT, PT || RQ и PT 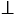 RT.
RT.
Начертим произвольный отрезок РQ.
Далее построим прямую параллельную PQ. Чтобы провести прямую параллельную отрезку РQ, прикладываем чертежный треугольник к отрезку PQ одной из его сторон образующих прямой угол, а вдоль другой стороны чертежного треугольника, образующей прямой угол, прикладываем линейку.

Не меняя положения линейки, двигаем вдоль нее чертежный треугольник на произвольное расстояние и проводим прямую вдоль стороны чертежного треугольника, которая и будет параллельна РQ.
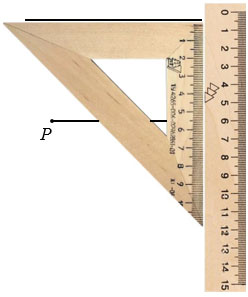
Теперь построим прямую PT перпендикулярную построенной прямой. Для этого прикладываем чертежный треугольник к построенной прямой одной из его сторон, образующих прямой угол, при этом точка Р должна лежать вдоль другой стороны чертежного треугольника, образующей прямой угол. Проводим отрезок от точки Р до прямой параллельной отрезку РQ вдоль стороны чертежного треугольника, полученную точку пересечения обозначаем буквой Т.
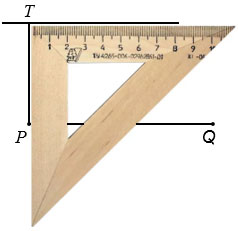
Мы знаем, что две прямые на плоскости перпендикулярные третьей прямой параллельны. Поэтому построим прямую RQ перпендикулярную прямой, проходящей через точку Т и параллельную прямой РQ.
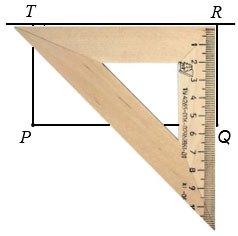
Убираем лишние части прямой TR.

РQRT - четырехугольник, у которого РQ || RT, PT || RQ и PT 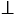 RT.
RT.
Вернуться к содержанию учебника