Задание 3.350 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 1. Страница 120
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№3.350 учебника 2023-2024 (стр. 120):
Каждое из чисел 220 и 284 равно сумме делителей другого числа, не считая его самого. Проверьте это утверждение.
№3.350 учебника 2021-2022 (стр. 120):
Каждое из чисел 6, 28, 496 равно сумме всех его делителей, не считая самого числа. Проверьте это утверждение. Такие числа называют совершенными. Следующее совершенное число 8128.
Подсказка
№3.350 учебника 2023-2024 (стр. 120):
Вспомните:
- Делители и кратные.
- Сложение чисел.
№3.350 учебника 2021-2022 (стр. 120):
Вспомните:
- Делители и кратные.
- Сложение чисел.
Ответ
№3.350 учебника 2023-2024 (стр. 120):
Делители числа 220:
1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, 220.
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 +
+ 55 + 110 = 3 + 9 + 21 + 42 + 99 + 110 =
= 12 + 63 + 209 = 75 + 209 = 284 - верно.
Делители числа 284:
1, 2, 4, 71, 142, 284.
1 + 2 + 4 + 71 + 142 = 3 + 75 + 142 =
= 78 + 142 = 220 - верно.
| + | 1 | 4 | 2 |
| 7 | 8 | ||
| 2 | 2 | 0 |
Пояснения:
Натуральное число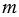 
делится без остатка на натуральное число 
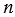, если есть такое число 
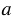, что 
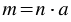. Натуральное число 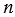называют делителем натурального числа 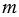, а число 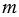- кратным числа .
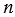№3.350 учебника 2021-2022 (стр. 120):
Делители числа 6: 1, 2, 3, 6.
1 + 2 + 3 = 6 - верно.
Делители числа 28: 1, 2, 4, 7, 14, 28.
1 + 2 + 4 + 7 + 14 = 28 - верно.
Делители числа 496:
1, 2, 4, 8, 16, 31, 62, 124, 248, 496.
1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248=
= 15 + 47 + 186 + 248 = 62 + 186 + 248 =
= 248 + 248 = 496 - верно.
|
|
Пояснения:
Натуральное число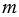 
делится без остатка на натуральное число 
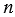, если есть такое число 
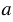, что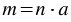 
. Натуральное число 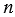называют делителем натурального числа 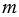, а число 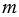- кратным числа .
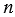Вернуться к содержанию учебника