Страница 47 - ГДЗ Математика 2 класс. Моро, Бантова. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
1. К каждому примеру на умножение составь два примера на деление.
| 4 • 3 = 12 | 6 • 5 = 30 | 10 • 2 = 20 |
12 : 4 =  |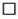
30 : 6 = |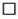
20 : 10 = |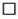
| 12 : 3 = |
30 : 5 = |
20 : 2 = |
Подсказка
Если произведение двух множителей, разделить на один из них, то получится другой множитель.
Ответ
Вопрос
2. 
4 • 7  4 • 9 |
20 • 3 3 • 20 |
| 0 • 5 1 • 4 |
6 • 2 6 + 6 |
| 2 • 7 2 • 6 |
12 + 0 12 - 0 |
Подсказка
От перестановки множителей результат умножения не изменяется.
Если 1 умножить на число, получится то же самое число.
Если 0 умножить на число, получится 0.
Ответ
Решение
| 4 • 7 < 4 • 9 | 20 • 3 = 3 • 20 |
| 0 • 5 < 1 • 4 | 6 • 2 = 6 + 6 |
| 2 • 7 > 2 • 6 | 12 + 0 = 12 - 0 |
Пояснение
Произведение будет тем больше, чем больше множители в этом произведении. Если в произведениях один из множителей совпадает, то сравниваю произведения по вторым множителям.
|
4 • 7 < 4 • 9 7 < 9 |
20 • 3 = 3 • 20 перестановка мест |
|
0 • 5 < 1 • 4 0 < 4 |
6 • 2 = 6 + 6 по 6 взяли 2 раза |
|
2 • 7 > 2 • 6 7 > 6 |
12 + 0 = 12 - 0 12 = 12 |
Вопрос
3. 1) Цена тетради 3 р. Сколько стоят 5 таких тетрадей?
Сделай схематический чертёж и реши задачу.
2) Составь и реши задачи, обратные данной.
Подсказка
Сумму одинаковых слагаемых можно заменить умножением.
Ответ
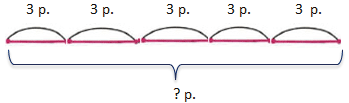
3 • 5 = 15 (р.)
Ответ: 15 рублей стоят тетради.
Обратная задача 1:
За 5 тетрадей заплатили 15 р. Сколько стоит одна такая тетрадь?
15 : 5 = 3 (р.)
Ответ: тетрадь стоит 3 рубля.
Обратная задача 2:
На 15 р. купили несколько тетрадей. Сколько тетрадей купили, если одна тетрадь стоит 3 рубля?
15 : 3 = 5 (т.)
Ответ: купили 5 тетрадей.
Вопрос
4. В киоске за день продали 50 тетрадей, а осталось на 27 тетрадей меньше, чем продали.
Сколько всего тетрадей было в киоске до продажи?
Подсказка
Повтори действия с двузначными числами.
Вспомни, как составить краткую запись задачи.
Ответ
Вопрос
5.
| 83 - 67 | 36 + 29 | 52 - 44 | 72 + 28 |
Подсказка
Ответ
Решение
|
|
|
|
Пояснение
Сложение и вычитание выполняем в столбик.
При выполнении вычитания в столбик, если единицы уменьшаемого меньше единиц вычитаемого, над десятками уменьшаемого ставим точку, чтобы не забыть о том, что один десяток забрали.
Если есть необходимость, то число, которое запоминают при выполнении сложения в столбик, можно писать сверху над разрядом, к которому это число будут прибавлять.
|
|
Вопрос
6.
| 90 - (48 - 6) | 64 + (18 + 2) | 8 + 9 - 7 |
| 60 - (52 - 2) | 70 - (9 + 9) | 6 + 7 - 8 |
Подсказка
Вспомни порядок выполнения действий при нахождении значения числовых выражений со скобками и без них.
Ответ
Решение
| 90 - (48 - 6) = 48 | 70 - (9 + 9) = 52 |
| 60 - (52 - 2) = 10 | 8 + 9 - 7 = 10 |
| 64 + (18 + 2) = 84 | 6 + 7 - 8 = 5 |
Пояснение
Если в выражении есть скобки, то сначала выполняют действия в скобках, а затем за скобками.
Если выражении нет скобок и оно содержит только действия сложения и вычитания, то действия выполняют по порядку слева направо.
|
90 - (48 - 6) = 90 - 42 = 90 - 40 - 2 = 50 - 2 = 48 |
70 - (9 + 9) = 70 - 18 = 70 - 10 - 8 = 60 - 8 = 52 |
|
60 - (52 - 2) = 60 - 50 = 10 |
8 + 9 - 7 = 17 - 7 = 10 |
|
64 + (18 + 2) = 64 + 20 = 84 |
6 + 7 - 8 = 13 - 8 = 13 - 3 - 5 = 10 - 5 = 5 |
Если есть необходимость, то при решении примеров в два действия, можно записывать промежуточные ответы при выполнении первого действия сверху карандашом над этим действием (у нас промежуточные ответы выделены красным цветом).
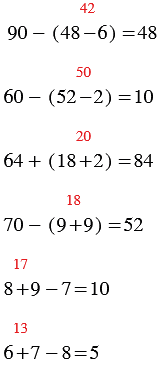
Вопрос
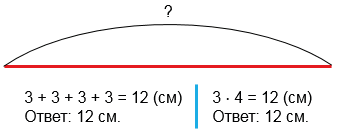
7. 1) Начерти в тетради такой квадрат.
2) Расскажи, что ты знаешь о квадрате, его сторонах, его углах, его осях симметрии.
3) Объясни, как по-разному ученики находили периметр этого квадрата:
Подсказка
Повтори материал о многоугольниках, вспомни, как найти периметр разными способами.
1 способ: Сложить длины всех сторон прямоугольника
2 способ: Умножить длину каждой стороны прямоугольника на 2 и найти сумму полученных произведений
3 способ: Сумму длин двух противоположных сторон прямоугольника умножить на 2.
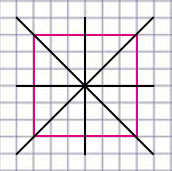
Ось симметрии фигуры - это прямая, которая делит фигуру на две симметричные части (если по этой прямой перегнуть фигуру, то ее части наложатся друг на друга).
Ответ
Решение
Вопрос 1:
Вопрос 2:
Прямоугольник, у которого все стороны равны и все углы прямые, называется квадратом. Квадрат имеет 4 оси симметрии.
Вопрос 3:
1 способ:
Нашли сумму всех сторон квадрата. Сложили длины всех сторон.
3 + 3 + 3 + 3 = 12 (см)
2 способ:
Длину одной стороны умножили на 4.
По 3 см взяли 4 раза.
3 • 4 = 12 (см)
Пояснение
Оси симметрии квадрата:
Также существуют и другие способы, чтобы найти периметр квадрата:
3 способ:
Умножить длину каждой стороны на 2 и найти сумму полученных произведений.
3 • 2 + 3 • 2 = 12 (см)
4 способ:
Сумму длин двух противоположных сторон прямоугольника умножить на 2.
(3 + 3 ) • 2 = 12 (см)
Вопрос
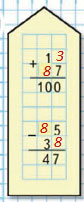
8. Вычисли и выполни проверку.
| 28 + 63 | 75 - 49 | 67 + 26 | 94 - 48 |
Подсказка
Ответ
| Решение | |||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
| Проверка | |||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Пояснение
Сложение и вычитание выполняем в столбик
При выполнении вычитания, если единицы уменьшаемого меньше единиц вычитаемого, над десятками уменьшаемого ставим точку, чтобы не забыть о том, что один десяток забрали.
Если есть необходимость, то число, которое запоминают при выполнении сложения в столбик, можно писать сверху над разрядом, к которому это число будут прибавлять. Например,
| 1 | ||
| + | 2 | 8 |
| 6 | 3 | |
| 9 | 1 |
Чтобы проверить сложение, можно использовать любой из следующих способов:
- из суммы вычесть первое слагаемое и в результате вычитания должно получиться второе слагаемое;
- из суммы вычесть второе слагаемое и в результате вычитания должно получиться первое слагаемое.
Чтобы проверить вычитание, можно использовать любой из следующих способов:
- к разности прибавить вычитаемое и в результате сложения должно получиться уменьшаемое;
- из уменьшаемого вычесть разность и в результате вычитания должно получится вычитаемое.
Вопрос
5 • 4 =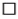 
20 : 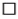= 5
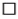: 4 = 5
4 • 5 =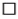
Подсказка
Ответ
5 • 4 = 20
20 : 4 = 5
20 : 4 = 5
4 • 5 = 20
Пояснение
Умножение чисел можно заменить сложением одинаковых слагаемых, в котором слагаемое - первый множитель, количество слагаемых - второй множитель.
5 • 4 = 5 + 5 + 5 + 5 = 20
Если произведение двух множителей разделить на один из них, то получится другой множитель.
20 : 4 = 5
20 : 4 = 5
От перемены мест множителей произведение не меняется.
4 • 5 = 20
Вопрос
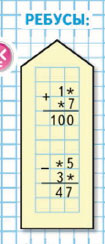
Подсказка
Вспомни действия с двузначными числами.
Вернуться к содержанию учебника