Задание 398 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№398 учебника 2013-2022 (стр. 107):
Постройте прямоугольную трапецию АВСD по основаниям и боковой стороне АD, перпендикулярной основаниям.
№398 учебника 2023-2024 (стр. 114):
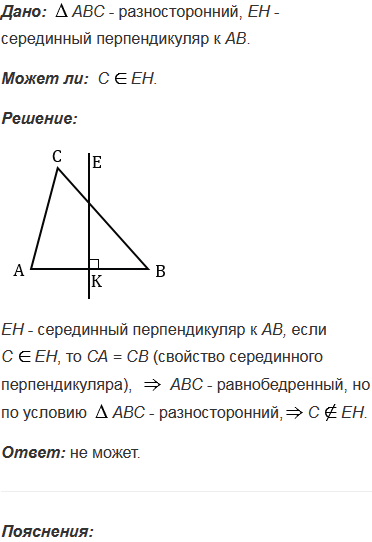
Может ли вершина разностороннего треугольника лежать на серединном перпендикуляре к какой-либо стороне? Ответ обоснуйте.
Подсказка
№398 учебника 2013-2022 (стр. 107):
Вспомните:
- Какая трапеция называется прямоугольной.
- Как построить отрезок, равный данному.
- Как построить перпендикулярные прямые.
№398 учебника 2023-2024 (стр. 114):
Вспомните:
- Какая фигура называется треугольником, разносторонний треугольник.
- Что такое серединный перпендикуляр к отрезку, его свойство.
- Какой треугольник называется равнобедренным.
Ответ
№398 учебника 2013-2022 (стр. 107):
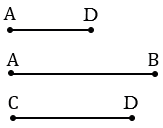
Дано: АВ и СD - основания, AD - трапеция.
Построить: прямоугольную трапецию АВСD.
Построение:
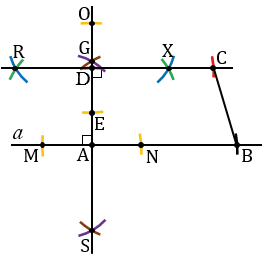
Построения:
Строим три отрезка АВ, СD, AD.

Строим прямую 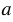 и отмечаем на ней точку А. С помощью циркуля измеряем отрезок АВ и строим окружность с центром в точке А радиуса АВ (всю окружность строить необязательно, смотри выделенное красным цветом), точку пересечения данной окружности с прямой
и отмечаем на ней точку А. С помощью циркуля измеряем отрезок АВ и строим окружность с центром в точке А радиуса АВ (всю окружность строить необязательно, смотри выделенное красным цветом), точку пересечения данной окружности с прямой 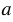 обозначаем буквой В.
обозначаем буквой В.
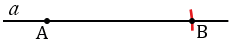
Далее, через точку А проведем перпендикуляр. Для этого строим окружность произвольного радиуса с центром в точке А (всю окружность строить необязательно, смотри выделенное желтым цветом). Точки пересечения данной окружности с прямой 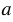 обозначаем буквами М и N. Затем, строим окружности радиуса МN с центрами в точках М и N (полностью окружности строить необязательно,смотри выделенное фиолетовым и коричневым цветом). Точки пересечения данных окружностей обозначаем буквами G и S. Проводим к прямой
обозначаем буквами М и N. Затем, строим окружности радиуса МN с центрами в точках М и N (полностью окружности строить необязательно,смотри выделенное фиолетовым и коричневым цветом). Точки пересечения данных окружностей обозначаем буквами G и S. Проводим к прямой 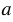 перпендикуляр GS.
перпендикуляр GS.
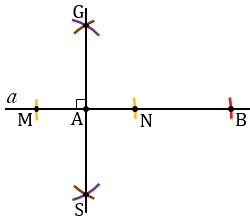
На луче АG от точки А откладываем отрезок, равный отрезку АD. Для этого строим окружность с центром в точке А радиуса АD (всю окружность строить необязательно, смотри выделенное красным цветом). Точку пересечения данной окружности с лучом АG обозначаем буквой D.
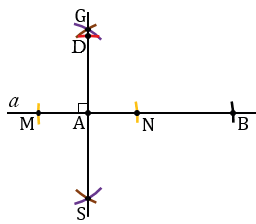
Далее проводим через точку D перпендикуляр к лучу АG. Для этого строим окружность произвольного радиуса с центром в точке D (всю окружность строить необязательно, смотри выделенное желтым цветом). Точки пересечения данной окружности с лучом АG обозначаем буквами О и Е. Затем, строим окружности радиуса ОЕ с центрами в точках О и Е (полностью окружности строить необязательно,смотри выделенное зеленым и синим цветом). Точки пересечения данных окружностей обозначаем буквами R и X. Проводим к лучу AG перпендикуляр RX.
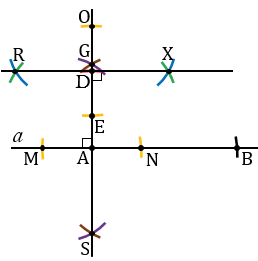
Теперь на луче DX откладываем от точки D отрезок, равный отрезку СD. Для этого строим окружность радиуса СD с центром в точке D (всю окружность строить необязательно, смотри выделенное красным цветом). Точку пересечения данной окружности с лучом DХ обозначаем буквой С. Соединяем точки В и С, Получаем четырехугольник АВСD, который является исходной прямоугольной трапецией по построению.

№398 учебника 2023-2024 (стр. 114):

Вернуться к содержанию учебника