Задание 6.42 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№6.42 учебника 2023-2024 (стр. 99):
Найдите два значения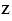 
, при которых верно двойное неравенство:
а) 5,42 < 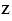< 9,76;
б) 0,3 < 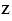< 0,4;
в) 3,6 < 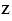< 3,7;
г) 14,99 < 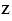< 15;
д) 8 < 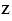< 8,01;
е) 1,123 < 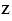< 1,124.
№6.42 учебника 2021-2022 (стр. 83):
Найдите два значения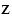 
, при которых верно неравенство:
а) 5,42 < 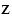< 9,76;
б) 0,3 < 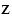< 0,4;
в) 3,6 < 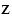< 3,7;
г) 14,99 < 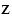< 15;
д) 8 < 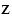< 8,01;
е) 1,123 < 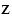< 1,124.
Подсказка
№6.42 учебника 2023-2024 (стр. 99):
№6.42 учебника 2021-2022 (стр. 83):
Вспомните:
- Десятичные дроби.
- Сравнение десятичных дробей.
Ответ
№6.42 учебника 2023-2024 (стр. 99):
№6.42 учебника 2021-2022 (стр. 83):
а) 5,42 <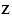 
< 9,76
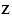= 7; 8.
б) 0,3 < 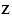< 0,4
0,30 < 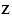< 0,40
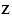= 0,31; 0,37.
в) 3,6 < 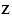< 3,7
3,60 < 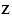< 3,70
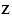= 3,64; 3,69.
г) 14,99 < 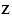< 15
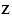14,990 < < 15
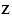= 14,991; 14,996.
д) 8 < 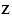< 8,01
8,000 < 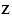< 8,010
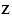= 8,003; 8,007.
е) 1,123 < 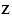< 1,124
1,1230 < 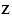< 1,1240
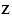= 1,1234; 1,1238.
Пояснения:
При сравнении десятичных дробей помним следующие правила:
1) если к десятичной дроби приписать справа нули или отбросить нули, то получится дробь, равная данной;
2) из двух десятичных дробей с разными целыми частями больше та дробь, у которой целая часть больше;
3) из двух десятичных дробей с одинаковыми целыми частями и равным количеством цифр после запятой больше будет та дробь, у которой больше первая (при чтении слева направо) из неодинаковых цифр их дробных частей (поразрядное сравнение);
4) чтобы сравнить две десятичные дроби с равными целыми частями и различным количеством цифр после запятой, надо с помощью приписывания нулей справа уравнять количество цифр в дробных частях, после чего сравнить полученные дроби поразрядно.
Вернуться к содержанию учебника