Задание 1523 - ГДЗ Математика 5 класс. Виленкин, Жохов, Чесноков. Учебник. Страница 229

В двоичной системе счисления при записи числа используют всего две цифры: 0 и 1. Число "один" записывается, как обычно, 1, но число "два" составляет уже единицу второго разряда и поэтому записывается так: 10₂ "одна двойка и нуль единиц" (цифра 2, находящаяся внизу в конце записи числа, означает, что число записано в двоичной системе). Число "три" изображается 11₂ "одна двойка и одна единица". Число "четыре" представляет собой единицу следующего, третьего разряда и поэтому записывается так: 100₂ "одна четверка, нуль двоек и нуль единиц". Таким образом, если в записи числа цифру 1 передвинуть влево на один разряд, то ее значение увеличивается вдвое (а не в десять раз, как в нашей десятичной системе). Сравните представление числа, запись которого состоит из четырех цифр 1, в виде суммы разрядных единиц в десятичной и двоичной системах:

1111 = 1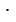1000 + 1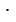100 + 1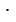10 + 1 = 1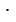10³ + 1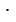10² + 1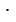10 + 1;

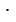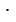1111₂ = 18 + 14 + 1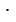 2 + 1 = 1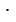2³ + 1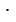2² + 1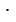2 + 1 = 15.

Попробуйте записать в десятичной системе счисления числа, которые в двоичной системе пишутся так: 10₂; 100₂; 101₂; 110₂; 1110₂.

Запишите в двоичной системе все натуральные числа от 1 до 15 включительно.

Подумайте, почему двоичная система широко используется в вычислительной технике, но она неудобна в повседневной практике.