Задание 6.157 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№6.157 учебника 2023-2024 (стр. 115):
Сравните значения выражений 42 -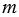 
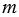или + 7,35, если 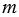равно 41,3; 2,649; 34,899; 17,325
№6.157 учебника 2021-2022 (стр. 99):
Какое из выражений 42 -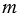 
или 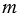+ 7,35 больше, если 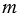равно 41,3; 2,649; 34,899; 17,325?
Подсказка
№6.157 учебника 2023-2024 (стр. 115):
№6.157 учебника 2021-2022 (стр. 99):
Вспомните:
- Числовые и буквенные выражения.
- Сложение и вычитание десятичных дробей.
- Сравнение десятичных дробей.
Ответ
№6.157 учебника 2023-2024 (стр. 115):
№6.157 учебника 2021-2022 (стр. 99):
1) Если 
= 41,3, то
42 - = 42 - 41,3 = 0,7
| • | ||||
| - | 4 | 2 | , | 0 |
| 4 | 1 | , | 3 | |
| 0 | , | 7 |
+ 7,35 = 41,3 + 7,35 = 48,65
| + | 4 | 1 | , | 3 | 0 |
| 7 | , | 3 | 5 | ||
| 4 | 8 | , | 6 | 5 |
0,7 < 48,65
(42 - ) < ( + 7,35) при = 41,3.
2) Если = 2,649, то
42 - = 42 - 2,649 = 39,351
| • | • | • | ||||
| - | 4 | 2 | , | 0 | 0 | 0 |
| 2 | , | 6 | 4 | 9 | ||
| 3 | 9 | , | 3 | 5 | 1 |
+ 7,35 = 2,649 + 7,35 = 9,999
| + | 2 | , | 6 | 4 | 9 |
| 7 | , | 3 | 5 | 0 | |
| 9 | , | 9 | 9 | 9 |
39,351 > 9,999
(42 - ) > ( + 7,35) при = 2,649.
3) Если = 34,899, то
42 - = 42 - 34,899 = 7,101
| • | • | • | • | |||
| - | 4 | 2 | , | 0 | 0 | 0 |
| 3 | 4 | , | 8 | 9 | 9 | |
| 7 | , | 1 | 0 | 1 |
+ 7,35 = 34,899 + 7,35 = 42,249
| + | 3 | 4 | , | 8 | 9 | 9 |
| 7 | , | 3 | 5 | 0 | ||
| 4 | 2 | , | 2 | 4 | 9 |
7,101 < 42,249
(42 - ) < ( + 7,35) при = 34,899.
4) Если = 17,325, то
42 - = 42 - 17,325 = 24,675
| • | • | • | • | |||
| - | 4 | 2 | , | 0 | 0 | 0 |
| 1 | 7 | , | 3 | 2 | 5 | |
| 2 | 4 | , | 6 | 7 | 5 |
+ 7,35 = 17,325 + 7,35 = 24,675
| + | 1 | 7 | , | 3 | 2 | 5 |
| 7 | , | 3 | 5 | 0 | ||
| 2 | 4 | , | 6 | 7 | 5 |
(42 - ) = ( + 7,35) при = 17,325.
Пояснения:
Чтобы найти значение буквенного выражение, нужно в это выражение вместо буквы подставить числа, ей соответствующие, и выполнить вычисления.
При вычислениях опираемся на следующее правило: чтобы сложить или вычесть десятичные дроби, нужно записать числа столбиком так, чтобы запятая стояла под запятой. Затем выполнить действие не обращая внимание на запятую, а в ответе поставить запятую под запятой. Также при вычислениях помним:
- если к десятичной дроби приписать справа какое угодно количество нулей, то получится дробь равная данной;
- если в десятичной дроби последние цифры - нули, то, отбросив их, получим дробь, равную данной;
- любое натуральное число можно представить в виде десятичной дроби с каким угодно количеством нулей после запятой.
При сравнении десятичных дробей опираемся на следующее правило: из двух десятичных дробей с разными целыми частями больше та дробь, у которой целая часть больше.
Вернуться к содержанию учебника