Номер 437 - ГДЗ Алгебра 8 класс. Мерзляк, Полонский. Учебник. Страница 108
Вернуться к содержанию учебника
Упражнения § 13. Страница 108
Вопрос
Петя и Коля ежедневно записывают по одному числу. В первый день каждый из мальчиков записал число 1. В каждый последующий день Петя записывает число 1, а Коля - число, равное сумме чисел, записанных мальчиками за предыдущие дни. Может ли в какой-то день Коля записать число, оканчивающееся на 101?
Подсказка
Вспомните, какие числа называют четными (нечетными).
Ответ
| Петя | Коля |
| 1 | 1 |
| 1 | 2 |
| 1 | 2 + 2 + 1 = 2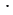 2 + 1= 5 2 + 1= 5 |
| 1 | 5 + 5 + 1 = 2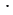 5 + 1 = 11 5 + 1 = 11 |
| 1 | 11 + 11 +1 = 2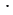 11 + 1 = 23 11 + 1 = 23 |
| 1 | ... |
| 1 | 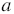 |
| 1 | 2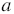 + 1 + 1 |
То есть если Коля запишет в какой-то день число , то на следующий день он запишет число 2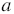 + 1, а сумма четного числа и нечетного есть число нечетное, то есть Коля с третьего дня всегда будет записывать нечетное число. Предположим, что Коля запишет число, которое заканчивается на 101, тогда в предыдущий день он записал число, которое заканчивается на (101 - 1) : 2 = 50, но 50 - число четное, но это противоречит тому, что начиная с третьего дня, Коля записывает только нечетные числа, то есть наше предположение неверно, и Коля не может записать число, которое заканчивается на 101.
+ 1, а сумма четного числа и нечетного есть число нечетное, то есть Коля с третьего дня всегда будет записывать нечетное число. Предположим, что Коля запишет число, которое заканчивается на 101, тогда в предыдущий день он записал число, которое заканчивается на (101 - 1) : 2 = 50, но 50 - число четное, но это противоречит тому, что начиная с третьего дня, Коля записывает только нечетные числа, то есть наше предположение неверно, и Коля не может записать число, которое заканчивается на 101.
Вернуться к содержанию учебника