Угол. Обозначение углов

Угол -  геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

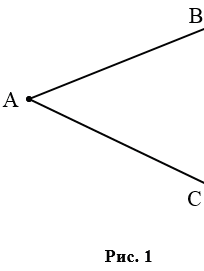
На рис. 1 лучи АВ и АС - стороны угла, точка А - вершина угла.

При записи угла в середине пишут букву, обозначающую его вершину. Сам угол на рис. 1 обозначают так: ВАС или САВ (этот угол нельзя обозначить так: АВС или СВА  или ВСА или  АСВ, т.к. точки В и С не являются вершинами данного угла). Этот же угол можно обозначить и короче, по его вершине: А.

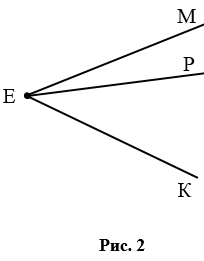
Если углы имеют общую вершину, то их нельзя обозначить одной буквой. Так на рис. 2 углы имеют общую вершину Е, поэтому мы можем использовать для данных углов только следующие обозначения: МЕК или КЕМ, МЕР или РЕМ, РЕК или КЕР. Говорят, что луч ЕР в данном случае делит угол МЕК (или КЕМ) на два угла: МЕР (или РЕМ) и РЕК (или КЕР).

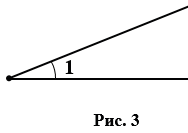
Также иногда углы обозначают цифрами, например, на рис.3 мы имеем 1.

Углы, как и отрезки, можно сравнивать между собой. Чтобы сравнить два угла можно наложить один угол на другой. Если при наложении одного угла на другой они совпадут, то эти углы равны.

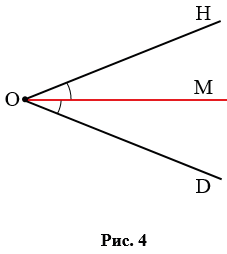
Биссектриса - луч, который делит угол на два равных угла. На рис. 4 углы НОМ и DОМ равны, значит, луч ОМ - биссектриса угла НОD.

Прямой угол - угол, который можно построить с помощью угольника (рис. 5).

Если начертить два прямых угла с общей вершиной и одной общей стороной, то две другие стороны этих углов составят прямую (рис. 6). Считают, что лучи, составляющие прямую, также образуют угол, который называют развернутым.

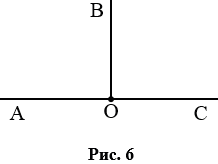
На рис. 6 АОВ и ВОС - прямые, АОС - развернутый.

Развернутый угол равен двум прямым углам, а прямой угол составляет половину развернутого.

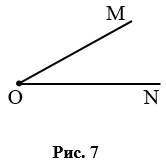
Острый угол - угол, который меньше прямого угла. На рис. 7 МОN - острый.

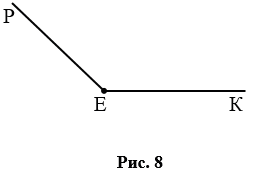
Тупой угол - угол, который больше прямого угла, но меньше развернутого. На рис. 8 РЕК - тупой.