Построение перпендикулярных прямых
Примеры:
1. Даны прямая и точка на ней. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.
Дано: прямая m, M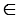 m.
m.
Построить: МP m.
m.
Решение:
Произвольно строим с помощью линейки прямую m и отмечаем на ней точку М.
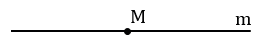
На лучах прямой m, исходящих из точки М, с помощью циркуля откладываем равные отрезки МА и МВ (МА = МВ). Для этого строим окружность с центром в точке М, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки М (смотри выделенное красным).
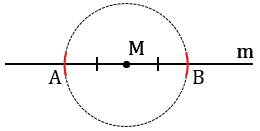
Затем строим две окружности с центрами в точках А и В радиуса АВ (полностью окружности строить необязательно, смотри выделенное фиолетовым и красным цветом).
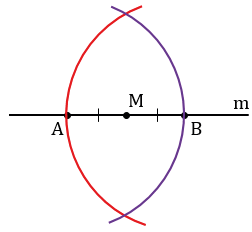
Данные окружности пересекаются в двух точках, обозначим их Р и Q. Проведем с помощью линейки через точку М и одну из точек Р или Q прямую, например, МР.
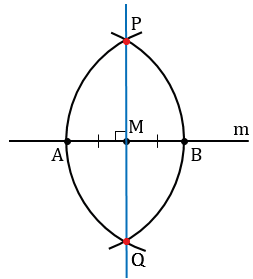
Докажем, что прямая МР - искомая прямая, т.е. что МP m.
m.
Рассмотрим треугольник АРВ.
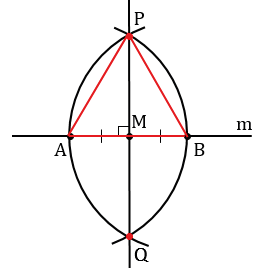
АР = ВР, т.к. по построению это радиусы одинаковых окружностей, следовательно,  АРВ - равнобедренный. По построению МА = МВ, т.е. МР - медиана равнобедренного треугольника, тогда по свойству равнобедренного треугольника МР и высота, т.е. МP
АРВ - равнобедренный. По построению МА = МВ, т.е. МР - медиана равнобедренного треугольника, тогда по свойству равнобедренного треугольника МР и высота, т.е. МP m. Что и требовалось доказать.
m. Что и требовалось доказать.
2. Даны прямая и точка не лежащая на этой прямой. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.
Дано: прямая m, M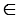 m.
m.
Построить: МN m.
m.
Решение:
Произвольно строим с помощью линейки прямую m и отмечаем точку М, не лежащую на прямой m.

Далее строим окружность с центром в данной точке М, пересекающую прямую m в двух точках, которые обозначим буквами А и В (всю окружность строить необязательно, смотри выделенное красным цветом).
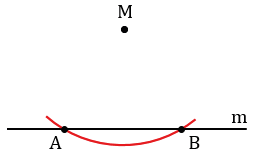
Затем построим две окружности с центрами в точках А и В, проходящие через точку М (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Эти окружности пересекутся в точке М и еще в одной точке, которую обозначим буквой N. Проведем прямую МN.
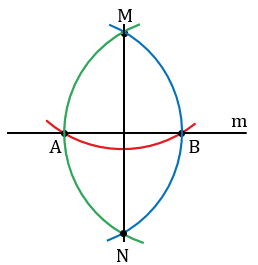
Докажем что, прямая МN - искомая, т.е. МN m.
m.
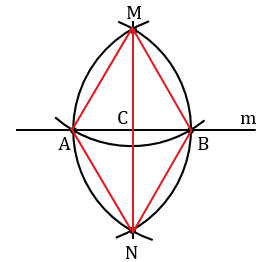
В  АМN и
АМN и  ВМN: АМ = АN = ВМ = ВN - радиусы, МN - общая, следовательно,
ВМN: АМ = АN = ВМ = ВN - радиусы, МN - общая, следовательно,  АМN =
АМN = ВМN (по трем сторонам), значит, углы ВМС и АМС равны (С точка пересечения прямых m и МN). Отсюда следует, что отрезок МС - биссектриса равнобедренного треугольника АМВ (АМ = ВМ - радиусы) с основанием АВ, тогда по свойству равнобедренного треугольника АМ - высота, значит, МN
ВМN (по трем сторонам), значит, углы ВМС и АМС равны (С точка пересечения прямых m и МN). Отсюда следует, что отрезок МС - биссектриса равнобедренного треугольника АМВ (АМ = ВМ - радиусы) с основанием АВ, тогда по свойству равнобедренного треугольника АМ - высота, значит, МN АВ, т.е. МN
АВ, т.е. МN m.
m.
Советуем посмотреть:
Построение угла, равного данному
Первый признак равенства треугольников
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Построения циркулем и линейкой
Правило встречается в следующих упражнениях:
7 класс
Задание 270, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 316*, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 317, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 395, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 398, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 900, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1145, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1171, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1283, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник